
Jogue quebra-cabeças Futoshiki online
No tutorial a seguir, técnicas básicas e avançadas para resolver quebra-cabeças de Futoshiki são apresentadas passo a passo, com ilustrações anexas para mostrar os métodos em configurações específicas do tabuleiro.
O ponto de partida para chegar a uma solução é a definição do jogo em si: o Futoshiki exige que o usuário descubra um tabuleiro em que cada dígito apareça uma vez em cada linha e coluna, respeitando as desigualdades dos tabuleiros. Usando esse critério, o progresso em direção a uma solução pode ser feito preenchendo, passo a passo, quadrados vazios do tabuleiro com dígitos específicos, pois são a única maneira de respeitar as restrições do tabuleiro.
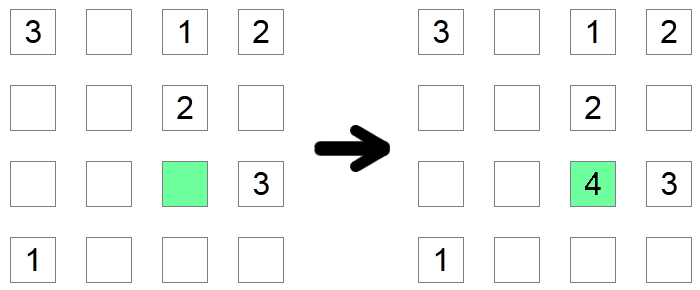
Se uma coluna e uma linha de quadrados já contiverem todos os dígitos possíveis, exceto um, esse quadrado deverá conter o dígito ausente. No exemplo acima, o quadrado verde deve ser 4, pois não seria permitido ter nenhum outro valor, pois os outros dígitos possíveis já estão em sua linha ou coluna.
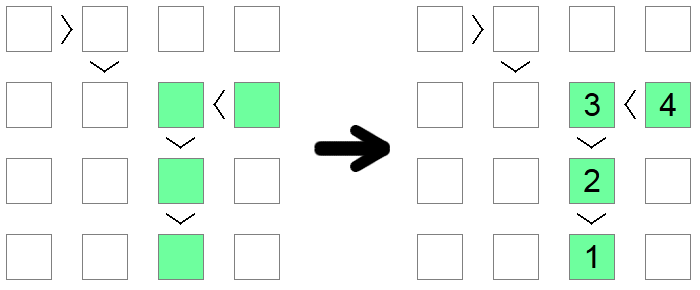
Se você notar uma cadeia de desigualdades, seja < (todas ascendentes) ou > (todas decrescentes), de tamanho igual ao tamanho das placas, essa cadeia deve ser uma sequência de 1 até o comprimento da placa. O comprimento da cadeia garante que essa sequência seja a única solução possível que satisfaça a condição monótona imposta pela cadeia de desigualdade.
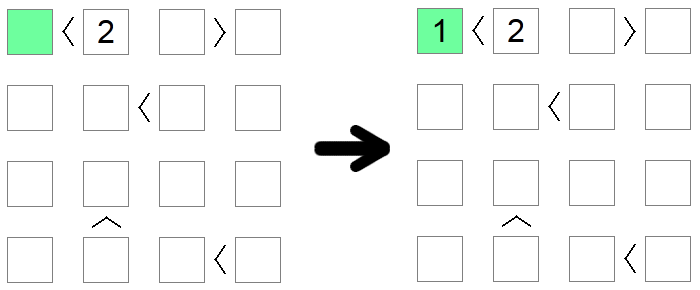
Quadrados menores que 2 devem ter implicitamente o valor 1, pois é o único valor admissível no tabuleiro que respeita essa condição. Da mesma forma, quadrados maiores que o tamanho do tabuleiro menos 1 devem ser iguais ao tamanho do tabuleiro. No exemplo acima, o único valor possível para o quadrado verde (menor que 2) é 1.
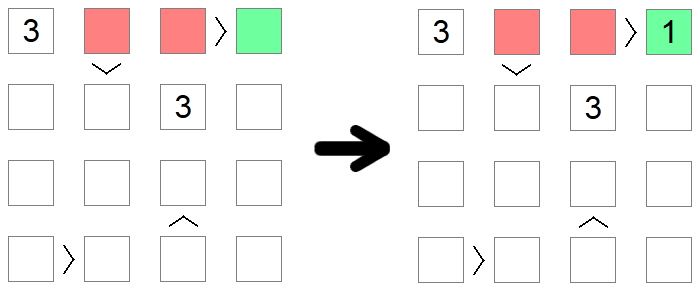
Quadrados maiores do que outros quadrados não podem ser 1, o menor valor permitido no tabuleiro, pois não há valor menor que 1. Da mesma forma, quadrados menores do que outros quadrados não podem conter o valor máximo permitido, pois não haveria nada maior a ser preenchido do outro lado da desigualdade. No exemplo acima, 1 não pode ser preenchido com os quadrados vermelhos, pois eles são todos maiores do que outros quadrados do tabuleiro, então a única colocação possível para 1 na primeira linha do tabuleiro é o quadrado verde.
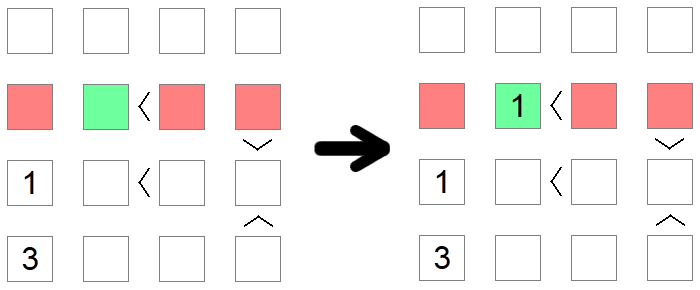
Às vezes, várias regras devem ser usadas para chegar a uma conclusão. Esse é o caso do exemplo acima, em que tentamos colocar o valor 1 na segunda linha do tabuleiro. O primeiro quadrado vermelho é eliminado devido à exclusão de uma coluna (já temos um 1 nessa coluna), enquanto o segundo e o terceiro quadrados vermelhos são eliminados devido à exclusão dos valores mínimos, pois esses lugares têm mais do que as desigualdades associadas a eles. Portanto, o quadrado verde continua sendo o único lugar possível para colocar 1 nessa linha.
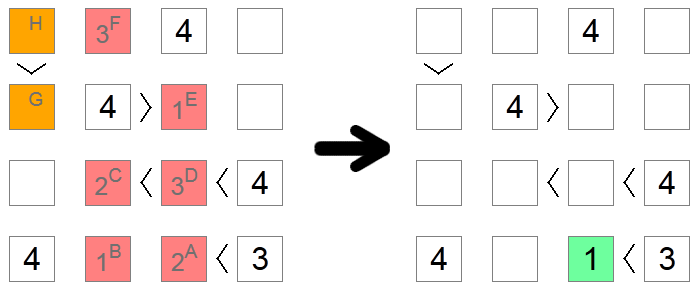
Às vezes, especialmente em quadros difíceis, não há outras maneiras de descobrir o dígito correto de um quadrado, exceto mergulhando nas implicações de cada possibilidade até que uma contradição seja alcançada. No exemplo acima, todos os quadrados vermelhos e laranja estão inicialmente em branco. Queremos descobrir se o quadrado A contém 1 ou 2. Assumimos que ele contém 2 e verificamos se chegamos a uma contradição com base nessa suposição.
Se o quadrado A tiver um 2, então o quadrado B teria um 1 (o único valor restante na linha inferior). O quadrado C pode ser 1 ou 2, pois tem uma cadeia de desigualdades que exige a disponibilidade de 2 números maiores, mas agora não pode ser 1 devido à exclusão da coluna do quadrado B, então o quadrado C é 2 e o quadrado D é 3 (o único valor entre 2 e 4). Devido às exclusões da coluna, o quadrado E é 1 e o quadrado F é 3.
Agora, se observarmos os quadrados laranja, notamos a contradição: se o quadrado G fosse 2, o quadrado H teria que ser 3 ou 4, o que não é permitido devido à exclusão de uma linha. Se o quadrado G fosse 3, o quadrado H teria que ser 4, o que não é permitido pelo mesmo motivo. Como não temos mais valores restantes para o quadrado G, isso significa que chegamos a um impasse e nossa suposição inicial estava errada: 2 não é um movimento válido para o quadrado A, então podemos seguir em frente e colocar 1 nele, o único outro valor possível.
Mostramos acima como resolver um quebra-cabeça de Futoshiki com sucesso, cobrindo uma variedade de técnicas que podem ajudá-lo a deduzir o próximo movimento, mesmo em situações difíceis. O outro ingrediente chave para se tornar proficiente e rápido na resolução de quebra-cabeças do Futoshiki é a experiência: quanto mais você pratica, melhor e mais rápido você se torna.
Se você está pronto para um desafio, você pode jogar agora mesmo um quebra-cabeça Futoshiki aleatório clicando no botão abaixo. Boa sorte!
© 2026 - Todos os direitos reservados - Sobre - Política de privacidade - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR